Centrado

Cálculo del centro de gravedad

PRIMERA PARTE: ¿DE QUE HABLAMOS?

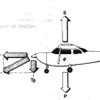
Todos hemos oído hablar de «donde está el centro de gravedad» o si «va adelantado o retrasado«. En propiedad, a efectos prácticos no científicos, debemos saber donde está ubicado en nuestro modelo ese famoso punto por lo importante que es para condicionar las características de vuelo. En los planos o instrucciones de un modelo debe figurar siempre su localización ( ver figura 2). El símbolo por el que se representa suele ser cualquiera de los tres representados en la figura 1. Los anglosajones suelen usar el central o el de la derecha pues además ellos se refieren a él como «Balance«. Nosotros usaremos el de la izquierda.

Vamos a enfocar el tema desde el punto de vista del «usuario» de un aeromodelo, no del de un diseñador. Así que sujetando, con los dedos mismos, nuestro modelo por la parte inferior del ala, intrados, a lo largo de la línea transversal al fuselaje a la altura del centro de gravedad observaremos que el aeromodelo se mantiene en equilibrio sin inclinarse claramente hacia el morro o la cola. Esta comprobación se hace con todo el equipo de radio y motor montados y el depósito de combustible vacío.

Debemos saber, no obstante que el punto referido lo condiciona exclusivamente el tipo de perfil alar y la forma, en planta ,del ala. Tampoco tiene una localización milimétrica pues hay un margen, según el perfil alar, dentro del que puede estar situado tal como indicamos en el cuadro adjunto ( figura 3 ). Fuera de ese margen no puede haber un vuelo estable. Dentro de él las posiciones más adelantadas darán un vuelo «pesado de morro» más seguro en un principio mientras vamos conociendo las reacciones del modelo. Si buscamos más maniobrabilidad, para vuelo acrobático por ejemplo, iremos a posiciones más retrasadas. Los cazas actuales carecen de estabilidad natural, están voluntariamente retrasados en su centrado y vuelan gracias a una computadora que interpreta y adecua las órdenes del piloto haciendo así posible el vuelo mediante ordenes electrónicas no mecánicas, lo que se entiende por «fly by wire«.

 

Figura 1. Símbolos usados para indicar la posición del «centro de gravedad», «punto de equilibrio» o de balanceo.

Piolín lo pasa fatal volando. Con ese cabezón tiene el C. de gravedad adelantado ¿Irá equipado con «Fly by wire«?

 

Figura 2	Figura 3. Posición del C.D.G. según tipo de perfil

SEGUNDA PARTE: COMO LOCALIZARLO

Ya hemos visto en la figura 3 la situación, según tipo de perfil, del c. de g.. Si tenemos un ALA RECTANGULAR, el ejemplo más sencillo posible, vemos como la cuerda (distancia según el eje longitudinal del avión  entre el borde de ataque -el anterior- y el de fuga -el posterior- del ala) es la misma desde la raíz al borde marginal, así que medimos el 30 % ( si es el % que corresponde a ese tipo de perfil) de esta cuerda a partir del borde de ataque. Una vez localizado el punto se hace desde él una perpendicular al eje longitudinal del avión y ahí estará localizado el centro de gravedad (figura 4). A lo largo de esta línea es donde colocaremos nuestros dedos para comprobar el antes referido balance.

Figura 4

En el caso de un ALA TRAPEZOIDAL debemos hallar la Cuerda Media (CM) también llamada Cuerda Media Aerodinámica (CMA). En cuanto a la longitud sabemos de antemano que es la media aritmética de la cuerda en la raíz de ala C-1 y la del extremo C-2 pero tenemos que localizarla geométricamente. Para ello dibujamos a tamaño natural o a escala la planta alar y trazamos una línea que una los dos puntos medios o centros geométricos (cg) de las dos cuerdas extremas. Después prolongamos a partir del borde de fuga, por ejemplo, la cuerda C-1 de la raiz en un valor igual a C-2. Haremos lo mismo en el marginal donde añadimos a C-2 una longitud igual a C-1 (figura 5). Unimos los dos extremos de esta prolongaciones con una línea que va a cortar a la que unía los dos cg y en esa intersección se halla la Cuerda Media o CM, como veis paralela al eje longitudinal del avión. Sobre ella medimos el % que corresponda al perfil y desde ahí trazamos una perpendicular al eje longitudinal del avión lo que nos dará la situación exacta del Centro de gravedad.

Figura 5. Ubicación del C.G. en un ala trapezoidal

 

ALAS EN FLECHA: Se calcula exactamente del mismo modo que en las trapezoidales. Lo único a destacar es lo retrasado que queda el centro de gravedad comparado con las rectangulares de ahí que los aviones con ala en flecha tengan el morro tan corto.

 

Figura 6. Cálculo del c.g. en un ala en flecha

ALAS EN DOBLE TRAPECIO: Aunque os suene raro es un tipo de ala (figura 7) muy común en aviones reales y de R.C. Como el P-51 Mustang, Bonanza, en numerosas avionetas Piper o Cessna, etc. En este caso comenzamos por halla las CM de cada uno de los paneles (CM-1 y CM-2) lo que haremos como en el ejmplo del ala trapezoidal. Una vez conocidas las dos CM y localizados sus centros geométricos (CG1 y CG2) nos permitirá calcular las coordenadas (X e Y) del CG de la Cuerda Media de toda el ala (CM-T), poder dibujar ésta y colocar el centro de gravedad. Para ello usamos las siguientes fórmulas:

siendo S-1 y S-2 las superficies de cada uno de los paneles alares

Figura 7	Figura 8

No os pongáis así que la cosa va a peor

 

Con las fórmulas y el gráfico siguiente localizamos el centro geométrico total (CGT) a través del cálculo de sus coordenadas y podemos trazar la cuerda media total (CMT) como habíamos dicho antes. En el caso representado en el gráfico todos los valores de Y son iguales, pero en la mayoría de los casos no ocurrirá esto. Aparentemente complicado pero si observáis bien los gráficos no lo es tanto. Ah, recordaréis que el área de un trapecio es la semisuma de las bases por la altura.

Figura 9. Localización del centro de gravedad en un ala de doble trapecio

 

EN LOS BIPLANOS: Nos podemos encontrar dos casos diferentes, que las dos alas tengan la misma superficie o que sean diferentes (sesquiplanos).

En el primer caso, alas de idéntica cuerda y envergadura consideramos como si fuera un monoplano cuya CM sería la distancia entre el borde de ataque de la CM del ala más adelantada (suele ser la superior) y el borde de fuga de la CM del ala más retrasada. Teniendo esta cuerda medimos el % que corresponda, según perfil, y ya tenemos el centro de gravedad (figura 10).

 

Figura 10. Centro de gravedad en biplanos con alas idénticas

En los biplanos sesquiplanos (figura 11) es decir con alas de diferente superficie se aplica una fórmula sencilla, comparada con las anteriores. Se parte de calcular por separado la posición del centro de gravedad en cada una de las alas. La distancia que separa estos dos centros, en el plano horizontal, la llamamos «D»  y a la superficie de cada ala S-1 y S-2 respectivamente. Hallando el valor «d» que es la distancia , horizontal, entre la posición del centro de gravedad del ala superior y la posición del centro de gravedad conjunto de ambas alas.

 

 

Figura 11. Centro de gravedad en Biplanos sesquiplanos

AVIONES «CANARDS»: En este tipo de avión el estabilizador va por delante del ala y a efectos de sustentación hay que considerarlo como otra ala. Calcularemos la posición del teórico centro de gravedad del ala y del estabilizador así como sus respectivas superficies. Aplicando la fórmula abajo indicada donde D es la distancia entre los centros de gravedad de ala y estabilizador. «d» sería la distancia entre el c. de g. del ala y el C. de gravedad efectivo del avión. SA y SE son las superficies de ala y estabilizador.

 

Figura 12. Centro de gravedad en modelos «canards»